Abstract

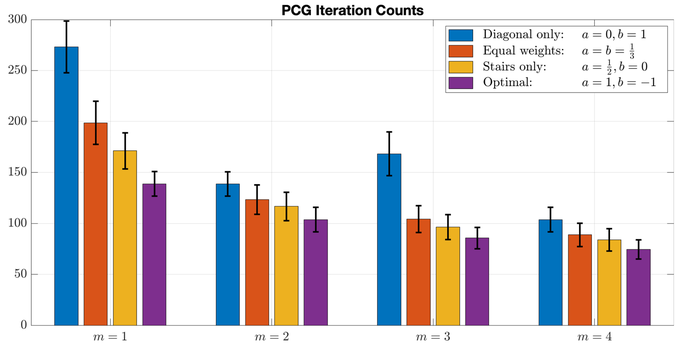
The efficient solution of moderately large-scale linear systems arising from the KKT conditions in optimal control problems (OCPs) is a critical challenge in robotics. With the stagnation of Moore’s law, there is growing interest in leveraging GPU-accelerated iterative methods, and corresponding parallel preconditioners, to overcome these computational challenges. To improve the performance of such solvers, we introduce a parallel-friendly, parametrized multi-splitting polynomial preconditioner framework. We first construct and prove the optimal parametrization theoretically in terms of the least amount of distinct eigenvalues and the narrowest spectrum range. We then compare the theoretical time complexity of solving the linear system directly or iteratively. We finally show through numerical experiments how much the preconditioning improves the convergence of OCP linear systems solves.