Abstract
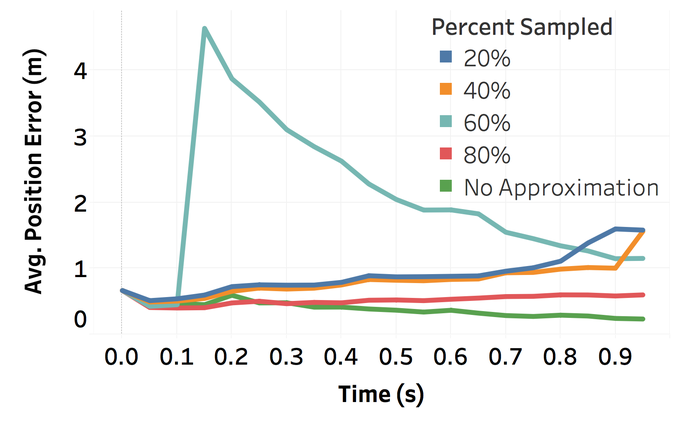
Computational efficiency is a critical constraint for a variety of cutting-edge real-time applications. In this work, we identify an opportunity to speed up the end-to-end runtime of two such compute bound applications by incorporating approximate linear algebra techniques. Particularly, we apply approximate matrix multiplication to artificial Neural Networks (NNs) for image classification and to the robotics problem of Distributed Simultaneous Localization and Mapping (DSLAM). Expanding upon recent sampling-based Monte Carlo approximation strategies for matrix multiplication, we develop updated theoretical bounds, and an adaptive error prediction strategy. We then apply these techniques in the context of NNs and DSLAM increasing the speed of both applications by 15-20% while maintaining a 97% classification accuracy for NNs running on the MNIST dataset and keeping the average robot position error under 1 meter (vs 0.32 meters for the exact solution). However, both applications experience variance in their results. This suggests that Monte Carlo matrix multiplication may be an effective technique to reduce the memory and computational burden of certain algorithms when used carefully, but more research is needed before these techniques can be widely used in practice.