Abstract

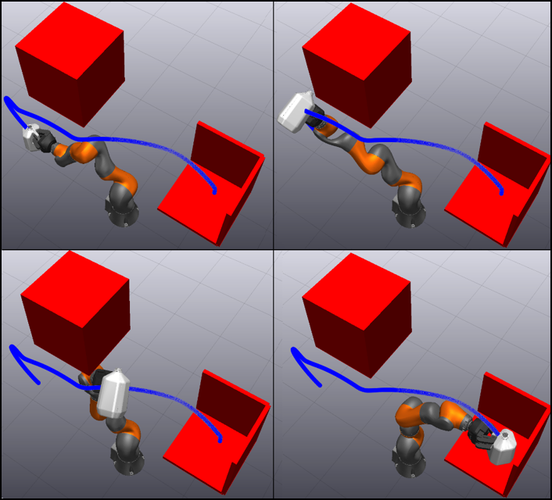
Differential Dynamic Programming (DDP) has become a popular approach to performing trajectory optimization for complex, underactuated robots. However, DDP presents two practical challenges. First, the evaluation of dynamics derivatives during optimization creates a computational bottleneck, particularly in implementations that capture second-order dynamic effects. Second, constraints on the states (e.g., boundary conditions, collision constraints, etc.) require additional care since the state trajectory is implicitly defined from the inputs and dynamics. This paper addresses both of these problems by building on recent work on Unscented Dynamic Programming (UDP) - which eliminates dynamics derivative computations in DDP - to support general nonlinear state and input constraints using an augmented Lagrangian. The resulting algorithm has the same computational cost as first-order penalty-based DDP variants, but can achieve constraint satisfaction to high precision without the numerical ill-conditioning associated with penalty methods. We present results demonstrating its favorable performance on several simulated robot systems including a quadrotor and 7-DoF robot arm.